"An idea whose time has come"- why do independent discoveries happen
I've been watching The Mindscape of Alan Moore, and I recommend you do too. I love Alan Moore. He's a particular mix of crazy and lucid that's always interesting to watch, even when not entirely agreeing with him, and in The Mindscape, he hints at a kind of philosophical approach to the world that's both infused by magical thinking and materialistic rationality. There will be more on that particular mix in this blog, a kind of ongoing project of the BLAND Corporation, but the inspiration is Moore and it is fitting that one of the first posts here is dedicated to discussing one of the ideas Moore puts forth in that film.
Here it is:
Moore never quite says so explicitly, but it appears he is suggesting that the idea space is something that can be interacted with. After all, you can leave stuff in the street for others to take. And looking at his understanding of Sheldrake's morphogenetic field, that interpretation becomes more likely. After all, it is claimed there, that the mere fact that a form appears in the physical world somehow causes it to appear again elsewhere, and it does so via poorly understood, 'spooky' causal pathways that might not be constrained by physics as we understand it today.
See, this is an interesting kind of crazy, because it suggests something to investigate. Surely there are simpler explanations for the nigh-simultaneous invention of the steam engine. If indeed such a thing occurred, but that's not the point. Independent discovery and invention are a fact of scientific and technological progress. So let's invent a world in which a group of craftsmen is inventing things, and lets see how many of them, and in what time-frame, figure the steam engine out.
As it happens, I don't have the resources to simulate a planet full of people, so I'll simplify the model a bit. Suppose the world is a grid of 'workshops', who may invent new technology, or copy/steal some from their neighbors. A workshop may also forget or lose some piece of technology for whatever reason. And just like civilization simulation computer games, I'll invent a technological tree for the steam engine. Ok, ok, it's not the best most accurate tree for the real steam engine, nor is it the only possible avenue for discovery. Fine. Criticism accepted. The point of the tech tree is to encode that you can't really invent something without certain other, prerequisite discoveries having been made before. Imagining something is different from inventing it. One may have imagined that some day people would be able to talk to each other despite being miles apart, but without the knowledge of the laws of electromagnetism or some other pertinent physics, such ideas were too incoherent to materialize into something actually useful. Once we knew and understood a few things about electromagnetic waves, we could invent radios. Once we had some knowledge of lasers, we could invent fiber optics based communication.
You may have noticed that the tech tree is a lot like the Idea Space that Moore proposes, but it's a 'read-only' idea space. Things are waiting there to be discovered, but nothing can be put there for someone else to find via telepathy, nor removed. There is no telepathic communication in my grid of workshops, each workshop only sees its neighbors.
So let's say that during one year a workshop has a chance to invent any number of technologies that it already knew the prerequisites for since before the year started; there's a chance that it will steal neighboring technology that was available to the neighbor at the previous year's end, as long as the techie thief had the prerequisites for that tech since before the new year began. 'Neighbor' means a workshop that is located immediately to the left, or right, or above, or below, in the grid. Finally, a workshop has a chance to lose a technology in a year, as long as at the end of the previous year it had no technology that needed it as a prerequisite.
One can define a 'chance to discover', 'chance to forget' and 'chance to transfer' for each tech, and in any number of complex ways that may depend on whatever factors. But for this post, I'm keeping things simple. All chances are constant numbers, and the chances of discovery are all the same. Likewise, the chances of forgetting are all equal to each other for all technologies, and all chances for transfer are also the same.
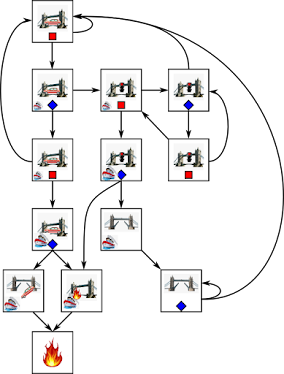
With that set up, let's do some simulations. I've attached a few animated gifs of a few sequences of simulation, and noted the parameters (the chances of various events) for each. A workshop is represented by a 3 by 3 grid, which is initially empty. When a technology is acquired, a place in the grid is occupied by a tiny icon. When the shop discovers the steam engine, the grid turns red. I end the simulation when at least five workshops have discovered the steam engine. To make following what's going on somewhat easier, I've made each year of the workshops last ten seconds. The gifs are fairly large resolution (1248 by 1248) and about half a meg each, hence the spoilerwall.
Here's a sequence for which the parameters (chances of various tech events) were: discover 0.1, forget 0.01, transfer 0.2.
Another, with parameters: discover 0.02, forget 0.01, transfer 0.2. Note that since discovery is slow here it takes a few more years for workshops to find a steam engine, but they tend to copy neighbours once they do. Even so, some independent discovery occurs.
Going the other way and emphasizing discovery for the next sequence, as parameters are: discover 0.2, forget 0.01, transfer 0.02. Steam engines quickly crop up all over the place, in independent discovery events.
As can be seen, the typical history of discovery has the shops rapidly increasing their know-how, and soon enough at least one will get a steam engine. Usually however, another one will discover a steam engine soon enough, even if it's not a neighbor of the original discoverer and therefore couldn't have stolen it. That may be true even when the chance for discovery is very small, but in general if the chance of discovery is small, and the chance of transfer large, then workshops that have the steam engine occur in clumps. Obviously, they're stealing from each other. If the chance of transfer isn't too big, and the chance of discovery isn't too small, then it's not unlikely for workshops that are very far apart, and not directly interacting, to discover the steam engine.
There's no morphogenetic field involved here. All that's going on are identical workshops trying to increase their know-how and all going at it at about the same pace. So if one workshop is especially rich in tech, chances are that's because it had the time to become rich in tech, and likewise other workshops had that time available and are rich in tech too.
I say 'almost the same pace' because one notices that workshops at the edges, and at the corners especially, tend to lag behind, especially when the chance of discovery is small and the chance of technology transfer is high. The reason should be obvious. Workshops on the edges and corners have fewer neighbors to steal tech from. Now, even if a workshop cannot be a first discoverer of the steam engine unless it actually discovers it on its own, the fact that it can steal tech along the way will speed up its progress and improve its chances to be a first discoverer.
So let's do another experiment. I ran 6000 simulations using one same parameter set emphasizing transfer, then another 6000 emphasizing discovery, and counted for each workshop position the times that it discovered the steam engine first. Next, I plotted the results in an image file. The lighter the pixel value, the larger that count. And indeed, if the chance of discovery is small, and that of transfer is large, then one can see how workshop positions closer to the center of the grid tend to be luckier. This effect is less noticeable if the chance of transfer is small, and vanishes if the transfer chance is zero.
I even added a situation in which there are obstacles inside the grid of workshops, preventing some workshops from communicating with each other, and you can see where the obstacles are by looking at the darker areas in that plot.
What's also apparent by looking at those statistical plots is that the further away a workshop is from the edges, the better its chance to be a first discoverer. Think about this for a minute. A workshop on a corner has two neighbors. A workshop on an edge has three. But any other workshop has four. So where's the difference coming from?
Well, it doesn't only matter how many neighbors a workshop has. If its neighbors also have many neighbors of their own, then they have a wide area to steal from, and so the original workshop may enjoy richer plunder in turn. Therefore, some kind of centrality measure is what one needs to look at, in order to see how well-placed a particular workshop is to be a technological leader. Browsing through my copy of "Dynamical Processes on Complex Networks", this looks a bit like 'degree centrality', the Bonacich power index version.
That daunting-sounding name simply means the number of neighbors, and the number of neighbors' neighbors, that a workshop has. It's not quite there though. The deeper a workshop is in the grid, or rather, the farther away it is from any edges (see the case where I added some extra obstacles to tech transfer between obstacles) the best it is at discovering the steam engine first. So I'd need something like neighbors, and neighbors' neighbors, and neighbors' neighbors' neighbors, and ...
But why bother with that, you'd say, if I have a neat way of measuring how apt a workhsop is to be the first discoverer simply by looking at the grid? It's because in the real world those workshops won't be on a grid. They'll be connected to each other in various ways, which are more easily representable as a random graph than a grid. Yes, it's more likely that neighbor will talk to neighbor. But there may be some special friendship with that other workshop over there yonder or there may be an enmity with the downstairs neighbor. And there's a load of difference between the two kinds of connection structures, grids and random graphs.
For one, I can't just look how far something is from the edge of the map in a random graph and decide how central it is. A workshop could be on the edge of the map, nonetheless it could be lucky enough to connect to everyone else. So I need a better measure of centrality for the case of random graphs.
But since this post is getting lengthy, and since that will require a rather different approach, I'll stop here for now. You see, I told you Alan Moore was interesting!
Here it is:
(1h:04m:42s) Alan Moore: "Rupert Sheldrake, who is a kind of heretical scientist, who put forward the idea of a morphogenetic field in order to try and understand some of the spookier effects of consciousness. I'm probably simplifying it horribly here, but I think that the basic concept was that once a form has occurred, whether that be a physical form or an idea form, then it is much more likely and possible for it to occur again.
Now, Sheldrake says that this is because of something he calls the morphogenetic field, linking everything, and that once the idea existed then it somehow existed in this morphogenetic field. It struck me that this might explain a lot of things about the way the human mind works, even things, for example, like the fact that the steam engine seems to have been invented by five or six different people at about the same time. After hundreds and thousands of years of the steam engine not being invented, in a matter of a couple of weeks everybody's, you know, it's steam engine time. {...}
This is similar to the idea that I've put forward of an 'idea space', a kind of, a space in which mental events can be said to occur, an idea space which is perhaps universal. Our individual consciousnesses have access to this vast universal space, just as we have individual houses but the street outside belongs to everybody. It's almost as if ideas are pre-existing forms within this space."
Moore never quite says so explicitly, but it appears he is suggesting that the idea space is something that can be interacted with. After all, you can leave stuff in the street for others to take. And looking at his understanding of Sheldrake's morphogenetic field, that interpretation becomes more likely. After all, it is claimed there, that the mere fact that a form appears in the physical world somehow causes it to appear again elsewhere, and it does so via poorly understood, 'spooky' causal pathways that might not be constrained by physics as we understand it today.
See, this is an interesting kind of crazy, because it suggests something to investigate. Surely there are simpler explanations for the nigh-simultaneous invention of the steam engine. If indeed such a thing occurred, but that's not the point. Independent discovery and invention are a fact of scientific and technological progress. So let's invent a world in which a group of craftsmen is inventing things, and lets see how many of them, and in what time-frame, figure the steam engine out.
As it happens, I don't have the resources to simulate a planet full of people, so I'll simplify the model a bit. Suppose the world is a grid of 'workshops', who may invent new technology, or copy/steal some from their neighbors. A workshop may also forget or lose some piece of technology for whatever reason. And just like civilization simulation computer games, I'll invent a technological tree for the steam engine. Ok, ok, it's not the best most accurate tree for the real steam engine, nor is it the only possible avenue for discovery. Fine. Criticism accepted. The point of the tech tree is to encode that you can't really invent something without certain other, prerequisite discoveries having been made before. Imagining something is different from inventing it. One may have imagined that some day people would be able to talk to each other despite being miles apart, but without the knowledge of the laws of electromagnetism or some other pertinent physics, such ideas were too incoherent to materialize into something actually useful. Once we knew and understood a few things about electromagnetic waves, we could invent radios. Once we had some knowledge of lasers, we could invent fiber optics based communication.
You may have noticed that the tech tree is a lot like the Idea Space that Moore proposes, but it's a 'read-only' idea space. Things are waiting there to be discovered, but nothing can be put there for someone else to find via telepathy, nor removed. There is no telepathic communication in my grid of workshops, each workshop only sees its neighbors.
So let's say that during one year a workshop has a chance to invent any number of technologies that it already knew the prerequisites for since before the year started; there's a chance that it will steal neighboring technology that was available to the neighbor at the previous year's end, as long as the techie thief had the prerequisites for that tech since before the new year began. 'Neighbor' means a workshop that is located immediately to the left, or right, or above, or below, in the grid. Finally, a workshop has a chance to lose a technology in a year, as long as at the end of the previous year it had no technology that needed it as a prerequisite.
One can define a 'chance to discover', 'chance to forget' and 'chance to transfer' for each tech, and in any number of complex ways that may depend on whatever factors. But for this post, I'm keeping things simple. All chances are constant numbers, and the chances of discovery are all the same. Likewise, the chances of forgetting are all equal to each other for all technologies, and all chances for transfer are also the same.
With that set up, let's do some simulations. I've attached a few animated gifs of a few sequences of simulation, and noted the parameters (the chances of various events) for each. A workshop is represented by a 3 by 3 grid, which is initially empty. When a technology is acquired, a place in the grid is occupied by a tiny icon. When the shop discovers the steam engine, the grid turns red. I end the simulation when at least five workshops have discovered the steam engine. To make following what's going on somewhat easier, I've made each year of the workshops last ten seconds. The gifs are fairly large resolution (1248 by 1248) and about half a meg each, hence the spoilerwall.
Here's a sequence for which the parameters (chances of various tech events) were: discover 0.1, forget 0.01, transfer 0.2.
» Click to show Spoiler - click again to hide... «
Another, with parameters: discover 0.02, forget 0.01, transfer 0.2. Note that since discovery is slow here it takes a few more years for workshops to find a steam engine, but they tend to copy neighbours once they do. Even so, some independent discovery occurs.
» Click to show Spoiler - click again to hide... «
Going the other way and emphasizing discovery for the next sequence, as parameters are: discover 0.2, forget 0.01, transfer 0.02. Steam engines quickly crop up all over the place, in independent discovery events.
» Click to show Spoiler - click again to hide... «
As can be seen, the typical history of discovery has the shops rapidly increasing their know-how, and soon enough at least one will get a steam engine. Usually however, another one will discover a steam engine soon enough, even if it's not a neighbor of the original discoverer and therefore couldn't have stolen it. That may be true even when the chance for discovery is very small, but in general if the chance of discovery is small, and the chance of transfer large, then workshops that have the steam engine occur in clumps. Obviously, they're stealing from each other. If the chance of transfer isn't too big, and the chance of discovery isn't too small, then it's not unlikely for workshops that are very far apart, and not directly interacting, to discover the steam engine.
There's no morphogenetic field involved here. All that's going on are identical workshops trying to increase their know-how and all going at it at about the same pace. So if one workshop is especially rich in tech, chances are that's because it had the time to become rich in tech, and likewise other workshops had that time available and are rich in tech too.
I say 'almost the same pace' because one notices that workshops at the edges, and at the corners especially, tend to lag behind, especially when the chance of discovery is small and the chance of technology transfer is high. The reason should be obvious. Workshops on the edges and corners have fewer neighbors to steal tech from. Now, even if a workshop cannot be a first discoverer of the steam engine unless it actually discovers it on its own, the fact that it can steal tech along the way will speed up its progress and improve its chances to be a first discoverer.
So let's do another experiment. I ran 6000 simulations using one same parameter set emphasizing transfer, then another 6000 emphasizing discovery, and counted for each workshop position the times that it discovered the steam engine first. Next, I plotted the results in an image file. The lighter the pixel value, the larger that count. And indeed, if the chance of discovery is small, and that of transfer is large, then one can see how workshop positions closer to the center of the grid tend to be luckier. This effect is less noticeable if the chance of transfer is small, and vanishes if the transfer chance is zero.
I even added a situation in which there are obstacles inside the grid of workshops, preventing some workshops from communicating with each other, and you can see where the obstacles are by looking at the darker areas in that plot.
What's also apparent by looking at those statistical plots is that the further away a workshop is from the edges, the better its chance to be a first discoverer. Think about this for a minute. A workshop on a corner has two neighbors. A workshop on an edge has three. But any other workshop has four. So where's the difference coming from?
Well, it doesn't only matter how many neighbors a workshop has. If its neighbors also have many neighbors of their own, then they have a wide area to steal from, and so the original workshop may enjoy richer plunder in turn. Therefore, some kind of centrality measure is what one needs to look at, in order to see how well-placed a particular workshop is to be a technological leader. Browsing through my copy of "Dynamical Processes on Complex Networks", this looks a bit like 'degree centrality', the Bonacich power index version.
That daunting-sounding name simply means the number of neighbors, and the number of neighbors' neighbors, that a workshop has. It's not quite there though. The deeper a workshop is in the grid, or rather, the farther away it is from any edges (see the case where I added some extra obstacles to tech transfer between obstacles) the best it is at discovering the steam engine first. So I'd need something like neighbors, and neighbors' neighbors, and neighbors' neighbors' neighbors, and ...
But why bother with that, you'd say, if I have a neat way of measuring how apt a workhsop is to be the first discoverer simply by looking at the grid? It's because in the real world those workshops won't be on a grid. They'll be connected to each other in various ways, which are more easily representable as a random graph than a grid. Yes, it's more likely that neighbor will talk to neighbor. But there may be some special friendship with that other workshop over there yonder or there may be an enmity with the downstairs neighbor. And there's a load of difference between the two kinds of connection structures, grids and random graphs.
For one, I can't just look how far something is from the edge of the map in a random graph and decide how central it is. A workshop could be on the edge of the map, nonetheless it could be lucky enough to connect to everyone else. So I need a better measure of centrality for the case of random graphs.
But since this post is getting lengthy, and since that will require a rather different approach, I'll stop here for now. You see, I told you Alan Moore was interesting!





Comments
Post a Comment