Parity Games: Intro

With computer software becoming more important and complex, finding and solving bugs is more critical and difficult than ever. But why must this be? Surely computer programs, running as they do on deterministic machines powered by pure math, can be checked automatically.

Well, in general, no. The space of programs, as a whole, is so wild that there exists no algorithm to answer even simple questions such as "will this get stuck in an endless loop".

But, if we only need to look at restricted classes of programs, there are mathematical methods to guarantee correctness, or automatically construct a correct program -- where "correct" of course depends on our application. Formal verification is the home of such nifty mathematics and in this post we will be looking at a beautiful slice of it: parity games.

Plus, parity games are the home of a tantalizing open question: are they solvable in polynomial time?

We'll define what "parity game" and "polynomial time" are in a moment, but first let's look at verification games more generally. Our overarching task is to develop some software or agent that responds appropriately -- whatever that means -- to challenges thrown by the world. Also, this agent or software will be fairly simple. It just looks at the state of the world, as described by a finite set of variables, and based on a collection of if-then rules, chooses one of a finite set of actions.

We will model the interaction between the agent and the world as a game, and, in particular, the games we will look at are:

    - zero-sum: the world is controlled by an evil genie who will punish any mistake of our agent. The genie wins if (and only if) it makes the agent behave inappropriately;

    - turn-based: the genie and agent do not act at the same time;

    - perfect information: both agent and genie know all there is to know about the state of the world.

Together, these are stringent and unrealistic constraints. There exist formal verification techniques to relax them, but in this post we will walk rather than run, and look at the basic verification games.

Here is a -- somewhat simplified and artificial -- example.

There is a drawbridge that car traffic can drive over when the bridge is down, or ships can cross through when the bridge is up. You can see when a ship is far away, but you cannot communicate with them at any time. Further, the ships' captains are as stubborn as their ships are massive. If a ship comes near the bridge, it will drive on and through no matter what. 

Our agent must control the bridge: clearing it of traffic and raising it, or lowering it. Obviously, a ship crashing into a lowered bridge is bad, and so is raising the bridge with traffic still on it.

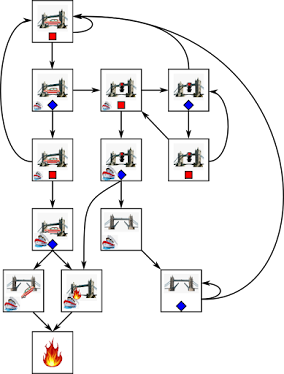
This toy problem has an obvious solution, but we'll work it out in detail. Let's list the possible world states and how they change into one another as a result of either the genie's or the agent's choices. Maybe there is no ship in the distance. The genie can choose to put a ship far away (this is drawn as a small ship), or keep the horizon clear. We mark the genie's choices with red squares.

With a ship in the distance, our agent can choose to clear car traffic from the bridge, or ignore this and do nothing. We mark our agent's choices with blue diamonds.

The genie wants to bring the game to the catastrophe state, marked with fire. If the genie succeeds, our agent loses -- it is not a safe agent to control the bridge. The two bad situations mentioned before -- ship crashing into the bridge or raising the bridge with traffic on it -- inescapably lead to this catastrophe state.

But also other states are bad because they inescapably lead the game to catastrophe. With a ship nearby and traffic still on the bridge, either choice of our agent is bad. So, when ALL our agent's options are bad, the state is bad.

Another state is when a ship is far away and traffic is still on the bridge. The genie could decide to have the far away ship just be passing by and disappear under the horizon again. But, being evil, the genie can bring the far away ship near and put our agent into a bad state. So, whenever ANY of the genie's choices leads to a bad state, that state is bad.

Reasoning like this we can discover all states from which the genie can force us into catastrophe regardless of what our agent does. This is known as an attractor, and the genie wins in this attractor with a positional strategy: from every vertex it controls in the attractor, the genie only needs one edge and may as well forget about its other options. Those edges in the game graph might as well not exist.

Outside the genie's attractor, our agent wins and can do so with a positional strategy of its own. The agent chooses one decision for each vertex and sticks to it, and its positional strategy wins because from here the genie has no paths to catastrophe. It is also easy to see how this positional strategy converts into a program made up of if-then rules that our agent can follow: if some conditions describing a state are true, then apply the action recommended by the positional strategy.

But safety isn't everything. Another strategy our agent can use is to never allow car traffic on the bridge. It ensures safety, but will annoy drivers wanting to use the bridge. Clearly, when designing programs we are often interested in properties such as requests being answered eventually, or states being always reachable. In other words, we often have more specifications for the behavior of our agents than just safety.

When we can model the agent-world interaction as a zero-sum, turn-based, perfect information game (plus another technical requirement called omega-regularity that is basically there so that we don't ask too much of a collection of if-then rules), all such behavior specifications on a program can be checked by parity games.

Parity games are played by two players, Even and Odd, who move a token on a graph. Either of them could be our agent; let's say Even is. As before, from some vertices Even chooses the next move, from the others Odd does. There will always be at least one next move possible. Finally, each vertex has a natural number, called a priority.

The players move the token forever. The winner is decided by the largest priority visited infinitely often by the token. Even wins if, and only if, this priority is Even.

I certainly felt this definition was strange when I first saw it. How can we decide a winner if the game never ends? What is the point of an eternal game?

Remember, we're interested in whether some piece of software will function correctly, for however long it will function. Everything dies eventually, but, not wanting to hardcode a lifespan limit, we abstract away from mortality. 

Just as an initial example, here is the bridge game from before now converted into a parity game. The catastrophe state just loops to itself and has an odd priority -- certainly, Odd wins if the game reaches this state. On the other hand, only the cars driving on bridge state has a high even priority, encouraging our agent to revisit this state forever. This captures both the safety requirement, and the requirement that the bridge should, sometimes, be a bridge.

That may explain the why of the definition, but how can we pick a winner in a neverending game? Recall the safe bridge controller game. Our agent wins it if this game lasts forever, but we don't need to wait that long for a proof. If the agent shows us a positional strategy that cuts off the current state from catastrophe, we can be certain it wins.

Something similar is true for parity games in general. Every game graph can be split into a region won by Even, and one by Odd -- though either winning region may be empty. The winning regions are determined: if a player has a strategy to win a region in a game, nothing the opponent can do will ever beat that strategy.

AND, all a player needs as a winning strategy is a positional strategy that eliminates all loops favorable to the opponent in the player's winning region. So, once Even commits to their winning strategy, there will be no loops where the maximum priority is odd in Even's winning region.

A priority showing up infinitely often, in a finite graph, means a vertex of that priority is visited infinitely often. If that vertex has the highest priority visited infinitely often, it must be the largest on the visited loops. Then, if Even can show such a positional strategy that leaves no Odd loops, there is no way for Odd to pass an infinte number of times through an Odd priority without some greater Even priority showing up.

Now, to show that for every parity game and every player, a positional strategy will be enough for that player to win their winning region, we just need an algorithm to find the strategies. One of the simplest is the McNaughton-Zielonka algorithm, or McZ for short. Here is an outline of it.

First, let us define McZ for the smallest game, the empty graph. The correct thing to do is to return empty winning regions. That's what McZ does, so it's correct for games of size 0!

Let us suppose now that McZ can return winning positional strategies for every game with less than n vertices, and we will construct a version of McZ that does so for games of n vertices.

 And, to keep things somewhat grounded, let's have a look at McZ in action over an example parity game. I'll leave the parity game for our bridge controller to the reader ;) and use this one as an example instead:

First, McZ checks what is the largest priority and uses it to determine the perspective player. If the largest priority in the game is Even, Even becomes the perspective player and Odd the opponent. Vice-versa when the largest priority is Odd. We compute the perspective player attractor to the largest priority, which gives them a positional attractor strategy. Note however that the attractor only guarantees these priorities are visited once. It does not guarantee returning.

For our illustration game, the highest prority is 3 (odd) so it computes Odd's attractor to vertices of priority 3.

Let's keep it for later anyway, but now we call McZ on the smaller game, the subgame, that is outside this attractor. Because McZ is correct for smaller games, it will return parity game positional strategies for the players. For this example game, the strategies and winning regions in the subgame outside the attractor are:

In general though, one thing that can happen is the opponent losing every vertex outside the attractor. But then, the opponent loses everywhere: whenever they dive into the attractor to try and escape the loss, the current player responds by forcing the game through the largest priority, which favors them.

The other case, which the example game also fell into, is that the opponent can win at least part of the outside. If so we compute the opponent's attractor to this part. The opponent is guaranteed to win here, because they can force the game into a region where all loops favor them -- and, if the largest priorities favoring the current player are visited at all in this part of the game, the opponent can ensure they get visited at most once.

In our example, we now can guarantee that some vertices will be won by Even, and have another three vertices to decide.

For whatever vertices are left outside this opponent attractor, which is a smaller game, we call McZ again. We merge the resulting positional strategies with what we already know, and that's what we return for the full game. For our example game, this is the result:

So now with parity games defined, let's turn to the other special term in the open problem above: are parity games solvable in polynomial time?

An algorithm will take more steps on bigger problems. It is intuitive, and correct, to expect that if McZ takes, on average (or worst case), some number of steps for parity games of 30 vertices, that it will take more steps on average (or worst case respectively) for games of 60 vertices. But how many more steps?

Computational complexity is the area of mathematics that estimates how this number of steps grows for an algorithm. It could be, for example, that the number of steps (on average/worst case) doubles for every extra vertex. This is exponential growth, and is very bad: however long your algorithm takes for graphs of ten vertices, it will take about a million times more for graphs of 30 vertices.

So we want the number of steps to increase as slow as possible. Some such slow increases are provided by the polynomial functions: suppose the number of steps is proportional to the square of the number of vertices. Then you'd expect solving a game of 30 vertices to take about 9 times more steps than solving a game of 10 vertices. 9 times more, compared to one million times more -- it seems much better to have algorithms with polynomial increases in steps.

More generally, polynomial time algorithms are those where the number of steps increases proportionally to n to some constant power c, where n is a measure of the size of a problem such as the number of vertices in a parity game graph.

In practice, it is not always clear-cut that polynomial time algorithms are preferrable. Some algorithms that are worst case exponential turn out to be, most (but not all) of the time, faster. That said, a theoretical advantage is as often as not a practical advantage -- polynomial time algorithms are, actually, usually faster.

Plus, there is a certain charm to the idea of a polynomial algorithm because, if such an algorithm exists, it has to cleverly exploit some kind of mathematical structure, as opposed to brute force searching through possible solutions.

For parity games, McZ turns out to be one of the most efficient for parity games usually encountered in practice. However, we know of families of parity games that force it to take its worst case execution time, which is exponential in the number of distinct priorities. This means even smallish parity games might take a lot of time to solve.

Recently, several algorithms were published that improved the worst case to quasipolynomial time -- as in almost, but not quite polynomial. The number of steps they need to solve a game increases proportional to n to the log(n) for n being the number of vertices in a game graph.

Although initially appearing different, these algorithms all turned out to use the same kind of underlying mathematical structure. This structure turned out to be quite a strong unifying concept, as several other algorithms, including McZ, turned out to use versions of it as well and so could be improved to worst-case quasipolynomial time. 

However, despite its power and combinatorial beauty, this structure pretty much guarantees that any algorithm using it will not be polynomial time. However, the scrolling wheel gets tired, and this will have to be a topic for another post.