Counter-state machines, continued
In a previous post I illustrated a way to count how many strings there are in a formally defined "regular language". One question was, supposing the state machine that recognizes the language has states from which no accepting state is reachable; is its observability matrix still full rank? The answer is no, and here's an example of that, and how to work around it.
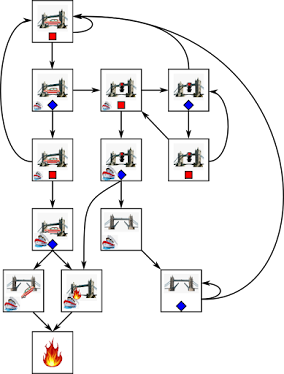
First, the regular language. Define the alphabet of symbols as "0" and "1", and the grammar rule is this: a finite string is in the language if and only if it contains no "11" substring. Thereafter, I'll use the notions introduced in that previous post. The resulting state machine is given below (initial state omitted), where the "_0" state corresponds to a string ending with "0" and "_1" corresponds to a string ending with "01". "meh" is a rejecting state, meaning the string contains a "11" substring.
I'll list states as "_0", "_1", "meh", and with that it's easy to convert the state diagram into a state transition matrix Ab, observation matrix Cb, and observability matrix Ob (all given below). As can be seen however, the observability matrix contains an all-0 column, meaning it is not full-rank and is not invertible.
However, not all is lost. Let's restrict the state transition and observation matrix to just the elements involving "_0" and "_1" states. The resulting observability matrix turns out to be invertible. Remember, this "restricted" state machine contains only two states, so the new observability matrix has only two rows. Further, the recurrence relation to give y[n] as a function of previous outputs is particularly simple: it is the Fibonacci recursion, where y[1] = 1 and y[2] = 2.
(Verifying, independently, that the number of n-bit strings that do not contain "11" is equal to the nth Fibonacci number in the sequence that starts with 1, 2 is left as an exercise for the reader.)
All this suggests a pattern: as long as the accepting states are reachable from a state in the machine, that state should be included in the calculation; if the accepting states are not reachable, then they will not matter and can be removed from the A,C,O matrices. At the moment, I didn't prove this; it's easy to see that if a state does not allow the machine to reach accepting states, then it will result in a 0 column in the observability matrix. The other side of the implication is less obvious, but doesn't seem too difficult, so I'll tackle it in the next few days.
First, the regular language. Define the alphabet of symbols as "0" and "1", and the grammar rule is this: a finite string is in the language if and only if it contains no "11" substring. Thereafter, I'll use the notions introduced in that previous post. The resulting state machine is given below (initial state omitted), where the "_0" state corresponds to a string ending with "0" and "_1" corresponds to a string ending with "01". "meh" is a rejecting state, meaning the string contains a "11" substring.
However, not all is lost. Let's restrict the state transition and observation matrix to just the elements involving "_0" and "_1" states. The resulting observability matrix turns out to be invertible. Remember, this "restricted" state machine contains only two states, so the new observability matrix has only two rows. Further, the recurrence relation to give y[n] as a function of previous outputs is particularly simple: it is the Fibonacci recursion, where y[1] = 1 and y[2] = 2.
(Verifying, independently, that the number of n-bit strings that do not contain "11" is equal to the nth Fibonacci number in the sequence that starts with 1, 2 is left as an exercise for the reader.)
All this suggests a pattern: as long as the accepting states are reachable from a state in the machine, that state should be included in the calculation; if the accepting states are not reachable, then they will not matter and can be removed from the A,C,O matrices. At the moment, I didn't prove this; it's easy to see that if a state does not allow the machine to reach accepting states, then it will result in a 0 column in the observability matrix. The other side of the implication is less obvious, but doesn't seem too difficult, so I'll tackle it in the next few days.
Comments
Post a Comment