Counter-State Machines
I've been doing Project Euler problems for the past couple of months (I'm BLANDCorporatio there too). It's very addicting, and I'm now at 151 solved (still 300+ to go, and they aren't getting any easier :P). Project Euler is great for exercising and learning some math, so if you like that and haven't heard of it, check it out.
Today I'll post about an imo neat concept I picked up while solving a few problems there. True, these are some of the easier ones I've tackled, but the concept itself has a cute elegance to it, and a decently wide scope of application, so I thought it makes for a good post.
I will not discuss Project Euler problems or solutions however. Where'd the fun be in solving them, if one just copied stuff?
So then, here's the type of problem I want to tackle: suppose you have some kind of mathematical object defined by a regular expression. Basically, that means the object is described by (or may be taken to be) some string of symbols, and the symbols obey the grammar described by the regular expression. The question is, how many objects are there, which are described by a string of length n, that is in the language defined by the grammar?
I'll use a very simple example as a toy problem. Suppose we only allow the symbols a,b,c,d,e,f,g,h and we are interested in knowing how many strings of length n contain at least one instance of the "abc" substring somewhere.
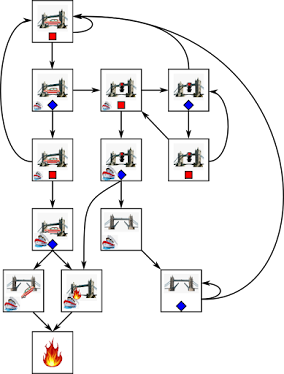
The thing about regular expressions/grammars/languages (these are used somewhat interchangeably) is that they can be recognized by a deterministic finite state machine. There exist algorithms to go from a regular grammar to a minimal state machine that recognizes it, so I won't bother with this step much. For the toy problem, it's easy to construct the state machine by hand. Here it is:
We have an initial state, and if the machine gets an "a" input symbol, it passes into the "_a" state (which we can interpret as, string ends in "a"). From state "_a" it can go to "_ab" if it gets a "b" input, and from there to "yay" if it gets a "c" input. "yay" is a so called accepting state; if a string of inputs causes the machine to reach an accepting state, it means the string obeys the regular expression.
There's also a "meh" state which corresponds to strings that don't have a particularly interesting suffix. The connections between the states (meaning, where the machine will go, based on current state and input) are fairly easy to understand for this problem. For more general problems, as I said, there are algorithms to go from regular expressions to an acceptor state machine.
Let us now change the semantics a little. Imagine the states of the machine are bags that contain strings. We will make it so that, at step n, a bag will contain the strings of length n that cause the original machine to go from the initial state to the state corresponding to the bag.
Initially, no bag contains any string, except, in a sense, the initial state bag which contains the empty string. (This distinction between empty string and no string at all is quite common in the theory of automata.)
When we get a symbol "a", we take strings from the bags- in the beginning, we have only one string in the initial state bag- and we append it to those strings. In this case, we get a string "a", which goes into the "_a" bag. If we received any of the b,c,d,e,f,g,h symbols, we would get strings to put into the "meh" bag.
That was the first step for the counter machine, so now the "_a" bag has one string ("a"), the "meh" bag has seven ("b", "c" etc), and all other bags are empty.
For the second step, let's see what we can do. If we added an "a" to strings from the "_a" bag, they would go back there (so now we'd have "aa" in the bag). If we added "b" to them, they'd go in the "_ab" bag (which now contains "ab" and nothing else). If we added anything else, they'd go into the "meh" bag. For strings in the "meh" bag, we can add "a" to them and put them in the "_a" bag, or, if we add anything else, back into the "meh" bag.
This suggests a pattern: how many strings will some bag X contain, at step n? The answer depends on the numbers of strings, at step n-1, in the bags that have an arrow towards bag X, and the dependecy is easy. If bag Y has m arrows towards bag X, then each string in bag Y at step n-1 contributes m strings to bag X at step n. The number of strings in bag X is simply the sum of contributions from bags that point to it.
This can be neatly captured in algebraic form by using matrices. Let x represent the 'state' (here, meaning number of strings in each bag). Let A be a transition matrix. If you have state at step n-1, then state at step n is simply A multiplied by that.
Also, let y[n] be the output (the number of strings at step n that obey the expression) and let C be an observation matrix. C is simply a row matrix where all elements are 0, except those that correspond to accepting states; those elements are 1. The reason for this is that the number of strings obeying the regular expression is the sum of the strings in the bags that correspond to accepting states. (The A and C notation is not arbitrary; it is meant to evoke the state space representation of dynamical systems, a problem which turns out to be very similar to this one.)
For the toy problem considered here, the matrices are given below. In state vectors, I listed the states as (initial, _a, _ab, yay, meh).
The i vector is the initial state of the machine (empty string in initial bag, no string in any other bag). I also showed what x[1], the state at step 1, would be.
Notice that to get the state at step n, you repeatedly multiply the A matrix to the initial state. This corresponds to matrix exponentiation. Apply the C matrix only once to get the output.
Technically, we're done. We have an answer to the problem, how many strings obey the expression, for any n we choose. There are libraries that will take care of matrix multiplication safely and efficiently, and it's not too shabby a solution. Besides, whatever regular expression we have, we can get a state machine, and whatever the state machine, we can unambiguously change it into a counter-state machine as described above. But, at least sometimes, we can do better.
I will rewrite the A and C matrices slightly, to remove the need for the initial state. It only matters for the first step, anyway, and it helps to have fewer states when doing this algebra. So suppose the initial state is x[1] = [1, 0, 0, 7] (transposed), where states are listed as "_a", "_ab", "yay", "meh". Rewriting the matrices means we remove the first row and first column of A, and the first column of C (or whatever corresponded to "ini").
The way to extract the state at step n, and the output, hasn't really changed (we just use x[1] as a base instead of i). Let us notice one thing however: we can write a sequence of outputs, for example those at steps n-1, n-2, n-3 and n-4, all from the state at step n-4. This is because if we know the counter-state machine state at n-4, we know it for all subsequent steps because Ab is constant, and we can compute all those other states.
So if we know x[n-4], we know all of y[n-1], y[n-2], y[n-3], y[n-4]. Suppose instead we somehow knew the ys instead though. Might we be able to compute x[n-4]? The answer is yes, provided the Mb matrix is invertible. Incidentally, I mentioned the connection between this problem and dynamical systems. Here it strikes again: the condition I described is precisely that for the observability of a dynamical system, i.e. the possibility to deduce its state at some time, based on a number of its outputs.
In our case, we have 4 states in the adjusted counter-state machine, so we need 4 outputs. In general, for a counter-state machine with m states, we will need m outputs.
Suppose then that Mb is invertible. Then we can write the output y[n] as
That matrix we multiply the ys with may look ugly in the expression, but actually it is a simplification. All the matrices involved in its construction are constant, so we can compute it once and be done with it, but also this matrix is actually a row vector. So instead of doing matrix multiplication to keep track of states, it is enough to sum the previous outputs, each multiplied by one number.
For our problem, this turns out to be y[n] = 16*y[n-1] - 64*y[n-2] - y[n-3] + 8*y[n-4].
This suggests a fairly simple procedure to count strings. Get y[1], y[2], y[3], and y[4] by using the counter-state machine as defined by the C and A matrices. Once you have these outputs known, use the coefficients you compute from the observability matrix of the adjusted counter-state machine.
Incidentally, the problem of counting the strings in a regular language has been tackled before, obviously. However, what wikipedia says about seems, to me, to be more confusing than enlightening. The counter-state machine approach is more intuitive, at least if you have some background with state space representations of dynamical systems, and the semantics of the counter-state machine justifies why the method of computation looks the way it does.
And counter-state machines do solve the general problem of counting the strings in a regular language, but this is also an interesting case of me knowing a solution, but still having more questions, regardless.
In particular, the observability matrix Mb. From a computation standpoint, all I need to know is whether it is invertible or not. But at the moment I can't link that to some graph-theoretic properties of the state machine. For example, suppose we had a non-accepting "sink" state. If a string causes the machine to enter this state, no subsequent suffix will ever make the machine reach an accepting state. (In our problem, we had an accepting sink; once the machine reaches "yay", it never leaves it). But, will a machine with non-accepting sinks also have an invertible observability matrix?
What about "source" states, states that the machine will never return to? The initial state was like this, but it was easy to get rid of. What if we have states that the machine will reach at some step, and then promptly leave, never to return to?
So there's some stuff to ponder here. There's also another thing to consider- there are many, many more languages than just regular ones. In fact, regular languages are rather weak in what they can describe, and stronger languages need other kinds of automata to recognize. Would a somewhat similar approach work, maybe at least for some of the simpler automata?
Today I'll post about an imo neat concept I picked up while solving a few problems there. True, these are some of the easier ones I've tackled, but the concept itself has a cute elegance to it, and a decently wide scope of application, so I thought it makes for a good post.
I will not discuss Project Euler problems or solutions however. Where'd the fun be in solving them, if one just copied stuff?
So then, here's the type of problem I want to tackle: suppose you have some kind of mathematical object defined by a regular expression. Basically, that means the object is described by (or may be taken to be) some string of symbols, and the symbols obey the grammar described by the regular expression. The question is, how many objects are there, which are described by a string of length n, that is in the language defined by the grammar?
I'll use a very simple example as a toy problem. Suppose we only allow the symbols a,b,c,d,e,f,g,h and we are interested in knowing how many strings of length n contain at least one instance of the "abc" substring somewhere.
The thing about regular expressions/grammars/languages (these are used somewhat interchangeably) is that they can be recognized by a deterministic finite state machine. There exist algorithms to go from a regular grammar to a minimal state machine that recognizes it, so I won't bother with this step much. For the toy problem, it's easy to construct the state machine by hand. Here it is:
We have an initial state, and if the machine gets an "a" input symbol, it passes into the "_a" state (which we can interpret as, string ends in "a"). From state "_a" it can go to "_ab" if it gets a "b" input, and from there to "yay" if it gets a "c" input. "yay" is a so called accepting state; if a string of inputs causes the machine to reach an accepting state, it means the string obeys the regular expression.
There's also a "meh" state which corresponds to strings that don't have a particularly interesting suffix. The connections between the states (meaning, where the machine will go, based on current state and input) are fairly easy to understand for this problem. For more general problems, as I said, there are algorithms to go from regular expressions to an acceptor state machine.
Let us now change the semantics a little. Imagine the states of the machine are bags that contain strings. We will make it so that, at step n, a bag will contain the strings of length n that cause the original machine to go from the initial state to the state corresponding to the bag.
Initially, no bag contains any string, except, in a sense, the initial state bag which contains the empty string. (This distinction between empty string and no string at all is quite common in the theory of automata.)
When we get a symbol "a", we take strings from the bags- in the beginning, we have only one string in the initial state bag- and we append it to those strings. In this case, we get a string "a", which goes into the "_a" bag. If we received any of the b,c,d,e,f,g,h symbols, we would get strings to put into the "meh" bag.
That was the first step for the counter machine, so now the "_a" bag has one string ("a"), the "meh" bag has seven ("b", "c" etc), and all other bags are empty.
For the second step, let's see what we can do. If we added an "a" to strings from the "_a" bag, they would go back there (so now we'd have "aa" in the bag). If we added "b" to them, they'd go in the "_ab" bag (which now contains "ab" and nothing else). If we added anything else, they'd go into the "meh" bag. For strings in the "meh" bag, we can add "a" to them and put them in the "_a" bag, or, if we add anything else, back into the "meh" bag.
This suggests a pattern: how many strings will some bag X contain, at step n? The answer depends on the numbers of strings, at step n-1, in the bags that have an arrow towards bag X, and the dependecy is easy. If bag Y has m arrows towards bag X, then each string in bag Y at step n-1 contributes m strings to bag X at step n. The number of strings in bag X is simply the sum of contributions from bags that point to it.
This can be neatly captured in algebraic form by using matrices. Let x represent the 'state' (here, meaning number of strings in each bag). Let A be a transition matrix. If you have state at step n-1, then state at step n is simply A multiplied by that.
Also, let y[n] be the output (the number of strings at step n that obey the expression) and let C be an observation matrix. C is simply a row matrix where all elements are 0, except those that correspond to accepting states; those elements are 1. The reason for this is that the number of strings obeying the regular expression is the sum of the strings in the bags that correspond to accepting states. (The A and C notation is not arbitrary; it is meant to evoke the state space representation of dynamical systems, a problem which turns out to be very similar to this one.)
For the toy problem considered here, the matrices are given below. In state vectors, I listed the states as (initial, _a, _ab, yay, meh).
The i vector is the initial state of the machine (empty string in initial bag, no string in any other bag). I also showed what x[1], the state at step 1, would be.
Notice that to get the state at step n, you repeatedly multiply the A matrix to the initial state. This corresponds to matrix exponentiation. Apply the C matrix only once to get the output.
Technically, we're done. We have an answer to the problem, how many strings obey the expression, for any n we choose. There are libraries that will take care of matrix multiplication safely and efficiently, and it's not too shabby a solution. Besides, whatever regular expression we have, we can get a state machine, and whatever the state machine, we can unambiguously change it into a counter-state machine as described above. But, at least sometimes, we can do better.
I will rewrite the A and C matrices slightly, to remove the need for the initial state. It only matters for the first step, anyway, and it helps to have fewer states when doing this algebra. So suppose the initial state is x[1] = [1, 0, 0, 7] (transposed), where states are listed as "_a", "_ab", "yay", "meh". Rewriting the matrices means we remove the first row and first column of A, and the first column of C (or whatever corresponded to "ini").
The way to extract the state at step n, and the output, hasn't really changed (we just use x[1] as a base instead of i). Let us notice one thing however: we can write a sequence of outputs, for example those at steps n-1, n-2, n-3 and n-4, all from the state at step n-4. This is because if we know the counter-state machine state at n-4, we know it for all subsequent steps because Ab is constant, and we can compute all those other states.
In our case, we have 4 states in the adjusted counter-state machine, so we need 4 outputs. In general, for a counter-state machine with m states, we will need m outputs.
Suppose then that Mb is invertible. Then we can write the output y[n] as
That matrix we multiply the ys with may look ugly in the expression, but actually it is a simplification. All the matrices involved in its construction are constant, so we can compute it once and be done with it, but also this matrix is actually a row vector. So instead of doing matrix multiplication to keep track of states, it is enough to sum the previous outputs, each multiplied by one number.
For our problem, this turns out to be y[n] = 16*y[n-1] - 64*y[n-2] - y[n-3] + 8*y[n-4].
This suggests a fairly simple procedure to count strings. Get y[1], y[2], y[3], and y[4] by using the counter-state machine as defined by the C and A matrices. Once you have these outputs known, use the coefficients you compute from the observability matrix of the adjusted counter-state machine.
Incidentally, the problem of counting the strings in a regular language has been tackled before, obviously. However, what wikipedia says about seems, to me, to be more confusing than enlightening. The counter-state machine approach is more intuitive, at least if you have some background with state space representations of dynamical systems, and the semantics of the counter-state machine justifies why the method of computation looks the way it does.
And counter-state machines do solve the general problem of counting the strings in a regular language, but this is also an interesting case of me knowing a solution, but still having more questions, regardless.
In particular, the observability matrix Mb. From a computation standpoint, all I need to know is whether it is invertible or not. But at the moment I can't link that to some graph-theoretic properties of the state machine. For example, suppose we had a non-accepting "sink" state. If a string causes the machine to enter this state, no subsequent suffix will ever make the machine reach an accepting state. (In our problem, we had an accepting sink; once the machine reaches "yay", it never leaves it). But, will a machine with non-accepting sinks also have an invertible observability matrix?
What about "source" states, states that the machine will never return to? The initial state was like this, but it was easy to get rid of. What if we have states that the machine will reach at some step, and then promptly leave, never to return to?
So there's some stuff to ponder here. There's also another thing to consider- there are many, many more languages than just regular ones. In fact, regular languages are rather weak in what they can describe, and stronger languages need other kinds of automata to recognize. Would a somewhat similar approach work, maybe at least for some of the simpler automata?
Comments
Post a Comment