What is reductionism
A friend sent me links to the Robert Sapolski lectures on biology and behavior, specifically the lecture about Chaos and Reductionism. Nice stuff, well worth watching. Though of course I wouldn't be me if I didn't notice that there were some things about those two topics that would need to be presented a bit differently.
So today, for Christmas, reductionism and how it manifests itself. The short answer for 'what is reductionism?' is, 'modular thinking applied to science'. For the long answer, use the read more link.
'Modular thinking' is an engineering/design approach, which says that when designing something, whatever it be, it helps to split it into parts, specify the allowed interactions between them, and thereafter design the parts independently. It's a very well-ingrained approach, but I'll still illustrate it on an example system.
I've chosen something that is complex, but not too complex- a pocket calculator. And while I won't go in so much detail so as to present the full blueprints of one, I will pursue it at some length- each of the various levels of modules is useful to show a point.
So, suppose you must design/build a pocket calculator; you were given indications about how big the thing should be, what kind of functions it should support etc. At this level, the calculator is just a black box, with buttons for inputs, a screen for output, and some specified input output behavior ("I want it to be able to add, subtract, multiply, divide, and do taxes, if respectively such and such sequences of buttons are pressed", say).
Since the project is a bit big, you assemble a team to help you out and divide design tasks between them. Someone needs to do the product design (how the thing actually looks), but for now I'll skip over that. You decide to split design tasks in a 'natural' fashion, according to the various functionality in the calculator: someone will design the button read electronics, someone the screen control circuits, someone the power supply and regulation, and finally (you may want a full team here) someone will take care of the stuff that actually does the calculation.
These blocks are specified by their interactions. The button electronics needs to send messages to the calculating block, such that the calculating block understands them correctly. Likewise, the calculating block needs to send messages to the screen control. All of those will require a certain amount of power from the power supply, further specifying things like voltage and max current, say.
Let's focus on the calculating block, which can further be divided into sub-blocks. No need to go through actually designing such a thing in this post, it's enough to notice that there are several distinct tasks the calculating block must do in order to fulfill its function. It needs to recognize which operation you are asking of it, for one; it needs to store the numbers while you type them; it needs to actually do the required operation on those numbers when you signal for it; and throughout it must send data to the screen.
So it's 'natural' to assign a 'part' in the block to each of those tasks, and as long as you specify how they fit together- what input language one expects, what it produces at output, what the general behavior is- you can then give different people the charge of designing each part on their own.
For example, take an adder circuit, which is simply some logic circuit which is given two numbers in binary as input, and produces their sum as output. Several adder designs exist; does your calculator have a ripple carry adder? Some kind of carry-look-ahead? As long as it adds correctly, provides timely results, obeys the input/output specification, nobody but the adder designer cares.
We can go deeper, and notice that the adder is made up of logic gates. A logic gate is a simple logic circuit that is given one or two bits as input and produces another bit as output, implementing a simple logic function like NOT ('1' becomes '0' and viceversa), AND (outputs '1' if both inputs are '1', outputs '0' otherwise) and so on. The adder designer, if you have one, will design the adder as a collection of gates connected in some way. They won't care what the logic gate circuit actually is.
If you have a logic gate designer, they might choose any of TTL, CMOS, and so on types of circuits, and each circuit is a collection of transistors connected in some way. The gate designer doesn't care much for the detailed design and construction of the transistors as long as he knows a transistor's behavior, and the transistors behave correctly.
So you can go even deeper at transistor level now, and see how changing various shape parameters affects the way in which the transistor behaves. Deeper than that is the level of electrons, where you might use Quantum Electro Dynamics to calculate how electrons will behave inside your transistor.
Having gone through all that excruciating detail, what should we notice?
The key advantage of modularity is that it allows one to split the work, but it's not the only one. If you designed a calculator today, you don't really need a transistor designer, or a logic gate designer, or even an adder designer. Those things have been designed ages ago, to well known specs, and are well tested. There are whole libraries of such designs that you can now drag and drop inside your project. As long as you feed those blocks the kinds of inputs they expect, and understand the kinds of outputs they provide, you're fine.
Another thing to notice is that a modular-designed system tends to look a certain way. Nature is, usually, 'messy'; things tend to diffuse in all directions, electromagnetic fields 'leak out' from wires, some oscillation here will produce an echo at that other place etc. Such things will happen in a modular system too, but unless an interaction is in the specification, it is deliberately -and visibly- minimized. If block A only sends output to block B, then no other block C will be sufficiently affected by the goings-on in A, so as to change its own behavior. Special structures will be put in place to keep parasitic influences to a minimum.
Also intrinsic in modularity is the requirement that 'this part does X'. This actually means two things; one, is that there is a functionality piece - structure piece correspondence that is one-one, or 'thereabouts'. The other thing it means, is that there exists an 'ideal', 'correct' behavior. If you know the specification, you already know what some part is 'meant' to do, and can treat differences between its specified and actual behavior as error. To illustrate, consider a NOT gate.
Ideally, as soon as the input changes, the output will change to the inverse of that. In reality that doesn't happen; there will be some delay before the output starts to react, and the change, when it happens, isn't instantaneous. Logic levels are represented by voltages, usually, and there's no getting around the fact that if you want to change a voltage level at some place, you will need to ferry some electric charge, through real wires that have resistance. And of course there's noise. The circuits will have to work around those problems; some mechanism of waiting for the result to happen needs to be implemented. Logic levels must be far enough apart that noise won't cause misreads.
So enough about modular design, what about reductionism?
It should first be clear that reductionism is not the same as saying, only the lowest level explanation is the true, valuable one. Only a strawman reductionist would be satisfied with an explanation like "the mind is just chemicals sloshing around", just like nobody would think they understand how a calculator works if they only knew it has to do with "electrons bumping into each other". Just as there are various levels of design, there are various levels of understanding and describing a system, and all are useful for various purposes. Even when the behavior is the result of many interactions between parts, one wants to think in terms of larger patterns; otherwise, there's no way to keep track of all the little things happening.
So then, imagine tackling the problem from the other direction to the one I've done before. You are given something, and must decide what it is, and find out how it behaves. If that thing you were given is a technological artifact, the name for what you are doing is reverse engineering, trying to infer the specification from the observed behavior. The reductionist approach in this case is nigh-guaranteed to be correct, because it's highly likely that the artifact was designed with modularity in mind. There is a specification for you to find, and the hallmarks of modularity in its structure will allow you to infer it, eventually.
There are some subtleties. If something is an 'error' of behavior sometimes, it doesn't follow that it's an error always. Consider the following circuit: two NOT gates in succession, and a XOR gate (which outputs '1' if one and only one of the inputs is '1').
Ideally, the circuit above is 'silly'. It will always output '0', because the two NOTs, one after the other, restore the input to its original value, and the input XOR itself is '0' (because anything XOR itself is '0'; the XOR must be fed inputs of different value to output '1').
BUT, the two NOTs are not ideal circuits. As shown above, there will be some time before the output of the first will react to a change in the input. The second NOT will insert a further delay. So the XOR isn't fed the same signal on its inputs; it is being fed the signal, and the signal with delay. The result is that when an 'edge' occurs on the input signal, the XOR will produce a brief '1' pulse. The circuit described above is an 'edge detector'.
That example is fairly technological, but it mirrors one from biology- how do neurons work? You could watch a neuron and see how it behaves as a function of its inputs, but what you are seeing there is a real system, with all the noise and messiness that implies. Are all the grooves and spikes in the output signal 'useful' for the brain? Are they noise that must be minimized? Or, in fact, what you are seeing is some clever use of imperfection as in the edge detector? The answer may be different for different neurons.
It appears that one problem with reductionism is that there is no blueprint, no specification, for natural systems. Unlike the reverse engineering a calculator (or whatever) case, there is no blueprint of the brain for you to find, so there is no a priori guarantee that a reductionist approach works.
In practice, many physical systems can be described in a modular fashion, because one can observe that certain interactions dominate the others; it's as if a specification existed, which required those interactions, while minimizing others. If the system being studied is not sensitive to tiny disturbances, it will behave 'as if' a specification existed.
I would say- other opinions and interpretations are available of course- that reductionism doesn't exactly fail if the system being studied is so sensitive to disturbance so as to make impossible to distinguish between 'noise' and 'desired' interactions. You simply need to add more to the list of interactions you consider important.
Take the heart. Inputs are nerve signals, oxygen and nutrients; output is mechanical work to pump blood. But wait, the heart is affected by the endocrine system, so add it to the list of inputs as well. What if kidneys don't work well, and toxins build up in the blood? Add those to the list of inputs too. And so on ... the problem now is that you have too much to track.
The goal of reductionism was to find the important interactions, so that you can focus on those and those alone. If it turns out all interactions are important, that's when you don't gain much from the approach.
One last comment, for now. A lot of issue was made in Sapolski's lecture about (non)linearity. Let's be clear about this, reductive/modular does not mean linear.
Linear is a system which, if you know its output to an input a (call the output x) and an input b (call it y), then you automatically know the output to n*a+m*b, because it's n*x+m*y. That's what a linear system is, no more no less.
There is no requirement that modules be linear. A power regulator circuit is not linear (though some are confusingly named such), because what a power regulator does is provide as constant an output as possible, despite changes in the input, which contradicts the linearity definition.
There is no requirement that reductionism be only applied to linear systems. Some nonlinear systems are very well behaved, the simple pendulum being an example.
What matters, as far as reductionism is concerned, is that there exist a correspondence between a piece of functionality and a piece of structure, which is enforced by the system being such that only a few of the interactions between its parts are actually relevant to determine the output, with the other interactions being parasitic noise that can be minimized/ignored.
So today, for Christmas, reductionism and how it manifests itself. The short answer for 'what is reductionism?' is, 'modular thinking applied to science'. For the long answer, use the read more link.
'Modular thinking' is an engineering/design approach, which says that when designing something, whatever it be, it helps to split it into parts, specify the allowed interactions between them, and thereafter design the parts independently. It's a very well-ingrained approach, but I'll still illustrate it on an example system.
I've chosen something that is complex, but not too complex- a pocket calculator. And while I won't go in so much detail so as to present the full blueprints of one, I will pursue it at some length- each of the various levels of modules is useful to show a point.
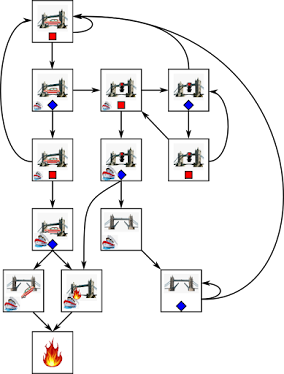
 |
| Levels of design- from finished product, to block diagram, down to transistors. |
So, suppose you must design/build a pocket calculator; you were given indications about how big the thing should be, what kind of functions it should support etc. At this level, the calculator is just a black box, with buttons for inputs, a screen for output, and some specified input output behavior ("I want it to be able to add, subtract, multiply, divide, and do taxes, if respectively such and such sequences of buttons are pressed", say).
Since the project is a bit big, you assemble a team to help you out and divide design tasks between them. Someone needs to do the product design (how the thing actually looks), but for now I'll skip over that. You decide to split design tasks in a 'natural' fashion, according to the various functionality in the calculator: someone will design the button read electronics, someone the screen control circuits, someone the power supply and regulation, and finally (you may want a full team here) someone will take care of the stuff that actually does the calculation.
These blocks are specified by their interactions. The button electronics needs to send messages to the calculating block, such that the calculating block understands them correctly. Likewise, the calculating block needs to send messages to the screen control. All of those will require a certain amount of power from the power supply, further specifying things like voltage and max current, say.
Let's focus on the calculating block, which can further be divided into sub-blocks. No need to go through actually designing such a thing in this post, it's enough to notice that there are several distinct tasks the calculating block must do in order to fulfill its function. It needs to recognize which operation you are asking of it, for one; it needs to store the numbers while you type them; it needs to actually do the required operation on those numbers when you signal for it; and throughout it must send data to the screen.
So it's 'natural' to assign a 'part' in the block to each of those tasks, and as long as you specify how they fit together- what input language one expects, what it produces at output, what the general behavior is- you can then give different people the charge of designing each part on their own.
For example, take an adder circuit, which is simply some logic circuit which is given two numbers in binary as input, and produces their sum as output. Several adder designs exist; does your calculator have a ripple carry adder? Some kind of carry-look-ahead? As long as it adds correctly, provides timely results, obeys the input/output specification, nobody but the adder designer cares.
We can go deeper, and notice that the adder is made up of logic gates. A logic gate is a simple logic circuit that is given one or two bits as input and produces another bit as output, implementing a simple logic function like NOT ('1' becomes '0' and viceversa), AND (outputs '1' if both inputs are '1', outputs '0' otherwise) and so on. The adder designer, if you have one, will design the adder as a collection of gates connected in some way. They won't care what the logic gate circuit actually is.
If you have a logic gate designer, they might choose any of TTL, CMOS, and so on types of circuits, and each circuit is a collection of transistors connected in some way. The gate designer doesn't care much for the detailed design and construction of the transistors as long as he knows a transistor's behavior, and the transistors behave correctly.
So you can go even deeper at transistor level now, and see how changing various shape parameters affects the way in which the transistor behaves. Deeper than that is the level of electrons, where you might use Quantum Electro Dynamics to calculate how electrons will behave inside your transistor.
Having gone through all that excruciating detail, what should we notice?
The key advantage of modularity is that it allows one to split the work, but it's not the only one. If you designed a calculator today, you don't really need a transistor designer, or a logic gate designer, or even an adder designer. Those things have been designed ages ago, to well known specs, and are well tested. There are whole libraries of such designs that you can now drag and drop inside your project. As long as you feed those blocks the kinds of inputs they expect, and understand the kinds of outputs they provide, you're fine.
Another thing to notice is that a modular-designed system tends to look a certain way. Nature is, usually, 'messy'; things tend to diffuse in all directions, electromagnetic fields 'leak out' from wires, some oscillation here will produce an echo at that other place etc. Such things will happen in a modular system too, but unless an interaction is in the specification, it is deliberately -and visibly- minimized. If block A only sends output to block B, then no other block C will be sufficiently affected by the goings-on in A, so as to change its own behavior. Special structures will be put in place to keep parasitic influences to a minimum.
Also intrinsic in modularity is the requirement that 'this part does X'. This actually means two things; one, is that there is a functionality piece - structure piece correspondence that is one-one, or 'thereabouts'. The other thing it means, is that there exists an 'ideal', 'correct' behavior. If you know the specification, you already know what some part is 'meant' to do, and can treat differences between its specified and actual behavior as error. To illustrate, consider a NOT gate.
 |
| Ideal vs. real signals. In reality, changes are not abrupt, and delays appear. |
Ideally, as soon as the input changes, the output will change to the inverse of that. In reality that doesn't happen; there will be some delay before the output starts to react, and the change, when it happens, isn't instantaneous. Logic levels are represented by voltages, usually, and there's no getting around the fact that if you want to change a voltage level at some place, you will need to ferry some electric charge, through real wires that have resistance. And of course there's noise. The circuits will have to work around those problems; some mechanism of waiting for the result to happen needs to be implemented. Logic levels must be far enough apart that noise won't cause misreads.
So enough about modular design, what about reductionism?
It should first be clear that reductionism is not the same as saying, only the lowest level explanation is the true, valuable one. Only a strawman reductionist would be satisfied with an explanation like "the mind is just chemicals sloshing around", just like nobody would think they understand how a calculator works if they only knew it has to do with "electrons bumping into each other". Just as there are various levels of design, there are various levels of understanding and describing a system, and all are useful for various purposes. Even when the behavior is the result of many interactions between parts, one wants to think in terms of larger patterns; otherwise, there's no way to keep track of all the little things happening.
So then, imagine tackling the problem from the other direction to the one I've done before. You are given something, and must decide what it is, and find out how it behaves. If that thing you were given is a technological artifact, the name for what you are doing is reverse engineering, trying to infer the specification from the observed behavior. The reductionist approach in this case is nigh-guaranteed to be correct, because it's highly likely that the artifact was designed with modularity in mind. There is a specification for you to find, and the hallmarks of modularity in its structure will allow you to infer it, eventually.
There are some subtleties. If something is an 'error' of behavior sometimes, it doesn't follow that it's an error always. Consider the following circuit: two NOT gates in succession, and a XOR gate (which outputs '1' if one and only one of the inputs is '1').
 |
| Edge detector: produces a short pulse when the input signal changes. This circuit would not work if the NOT gates were ideal (had no input/output delay). |
Ideally, the circuit above is 'silly'. It will always output '0', because the two NOTs, one after the other, restore the input to its original value, and the input XOR itself is '0' (because anything XOR itself is '0'; the XOR must be fed inputs of different value to output '1').
BUT, the two NOTs are not ideal circuits. As shown above, there will be some time before the output of the first will react to a change in the input. The second NOT will insert a further delay. So the XOR isn't fed the same signal on its inputs; it is being fed the signal, and the signal with delay. The result is that when an 'edge' occurs on the input signal, the XOR will produce a brief '1' pulse. The circuit described above is an 'edge detector'.
That example is fairly technological, but it mirrors one from biology- how do neurons work? You could watch a neuron and see how it behaves as a function of its inputs, but what you are seeing there is a real system, with all the noise and messiness that implies. Are all the grooves and spikes in the output signal 'useful' for the brain? Are they noise that must be minimized? Or, in fact, what you are seeing is some clever use of imperfection as in the edge detector? The answer may be different for different neurons.
It appears that one problem with reductionism is that there is no blueprint, no specification, for natural systems. Unlike the reverse engineering a calculator (or whatever) case, there is no blueprint of the brain for you to find, so there is no a priori guarantee that a reductionist approach works.
In practice, many physical systems can be described in a modular fashion, because one can observe that certain interactions dominate the others; it's as if a specification existed, which required those interactions, while minimizing others. If the system being studied is not sensitive to tiny disturbances, it will behave 'as if' a specification existed.
I would say- other opinions and interpretations are available of course- that reductionism doesn't exactly fail if the system being studied is so sensitive to disturbance so as to make impossible to distinguish between 'noise' and 'desired' interactions. You simply need to add more to the list of interactions you consider important.
Take the heart. Inputs are nerve signals, oxygen and nutrients; output is mechanical work to pump blood. But wait, the heart is affected by the endocrine system, so add it to the list of inputs as well. What if kidneys don't work well, and toxins build up in the blood? Add those to the list of inputs too. And so on ... the problem now is that you have too much to track.
The goal of reductionism was to find the important interactions, so that you can focus on those and those alone. If it turns out all interactions are important, that's when you don't gain much from the approach.
One last comment, for now. A lot of issue was made in Sapolski's lecture about (non)linearity. Let's be clear about this, reductive/modular does not mean linear.
Linear is a system which, if you know its output to an input a (call the output x) and an input b (call it y), then you automatically know the output to n*a+m*b, because it's n*x+m*y. That's what a linear system is, no more no less.
There is no requirement that modules be linear. A power regulator circuit is not linear (though some are confusingly named such), because what a power regulator does is provide as constant an output as possible, despite changes in the input, which contradicts the linearity definition.
There is no requirement that reductionism be only applied to linear systems. Some nonlinear systems are very well behaved, the simple pendulum being an example.
What matters, as far as reductionism is concerned, is that there exist a correspondence between a piece of functionality and a piece of structure, which is enforced by the system being such that only a few of the interactions between its parts are actually relevant to determine the output, with the other interactions being parasitic noise that can be minimized/ignored.
Comments
Post a Comment