A common knowledge puzzle
Here's a nifty gem of epistemic logic, a little puzzle that crops around in many forms. It appears at Terence Tao's blog, there's also an xkcd page about it, and there are several variations on it. Consider this one, simpler but complex enough to capture the subtlety: suppose there's a group of five aliens who are highly logical beings (whatever one can deduce, will be immediately deduced by that alien) but also rather quirky. None of them know the color of their own eyes, they don't speak with each other about eye colors, and they live where no reflective surfaces or such will ever tell them that information. So each alien knows only the colors of the others' eyes and not their own. If it matters, possible eye colors that the aliens know about are blue, green, red, black. As it happens, two out of the aliens in the group have blue eyes, and the remaining three have black eyes. A further quirk of these aliens: if ever one of them discovers the color of his/her own eyes, that alien will kill themselves on the next morning. One day, a troll visits the group of aliens and tells them "I see at least one of you has blue eyes." What happens?
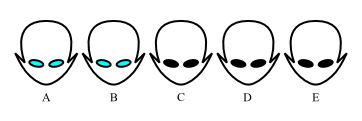
Just for fun a pretty picture of the situation: our five aliens, A, B, C, D, and E, each with their eye colors.
Now, what's interesting about the puzzle is that one can make two arguments about what happens. Both seem valid, but they can't both be, because their conclusions are contradictory. So one must be wrong, and it is interesting to see why.
I must stress, this is no 'lateral thinking'/'text lawyering' puzzle. It merely concerns itself with what the aliens can deduce from what the troll said. And even if a being that can deduce -every- consequence of something is implausible, that's not the point. These aliens can, so what will they do based on the information provided by the troll?
First answer is- nothing, because the troll gave them no information (ie, didn't tell them anything they didn't already know). "There's at least one blue eyed alien among you": well, each alien can see at least one blue-eyed alien. So all of them already know that what the troll said is true.
Second answer typically proceeds like this:
First thing to note is that often words mean more than what they appear to. Consider a very simple but enlightening scenario presented at the Stanford Encyclopedia of Philosophy: a waiter, as he passes you by, trips on something and spills drinks all over your expensive suit. Immediately the waiter says "I'm sorry, that was my fault" and dashes for a towel to dry you off. It's a pretty safe bet you're already blaming the waiter, and the waiter would know that you already think it's his fault. What you don't know is whether the waiter admits responsibility for clumsiness or is an irresponsible jerk. It's this uncertainty that his apology wants to dispel- the waiter wants you to know that the waiter also knows it was his fault.
Granted, he could have just said "I want you to know that I know that it was my fault", but human communication is often more subtle than meaning just what you say, as we've just seen.
Back to the puzzle. Let's imagine that we could look inside the mind of alien A and see what she knows. Obviously, she knows the eye colors of everyone else and doesn't know her own.
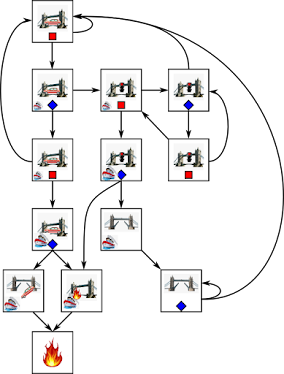
But actually, she knows a bit more. She knows that the other aliens are looking at each other, so she can deduce a few things about what they know, too. So let's update our diagram a bit ...
A few explanations on the drawing's conventions: whenever A knows something, she also knows that she knows that something, and knows that she knows that she knows etc. Since drawing this adds nothing but clutter, the part of the diagram that corresponds to A's self knowledge is marked red and left blank. Likewise, when A knows that B knows something, she also knows that B knows that B knows that something etc. So the part that corresponds to B's self knowledge, as assumed by A, is similarly marked red and left blank. It's trivial to fill these in if one wants to.
Notice also that I use question marks to say that somebody doesn't know their own color. Meanwhile, in the zone in which I drew A's knowledge of what B knows, I put white in B's knowledge of A's eye color. That's because A knows that B knows A's eye color, but what exactly that color is, A doesn't know.
And of course, A knows even more. We can expand that drawing to include knowledge about the knowledge about the knowledge of others. The interested reader may do this, but for this particular puzzle, this is not relevant.
Let's say now that, -before- the troll visited the aliens, we took A to one side, where no other alien is present, and asked her "do you know whether anyone of you has blue eyes"? Let's assume that since no other alien can hear her, the taboo against discussing eye colors is relaxed. Whatever. Her answer is, "yes, for example B has blue eyes."
That was easy. Let's say we asked instead, "what do you think C would answer if I asked him, do you know whether any one of you has blue eyes?". Look at the drawing above and see what A knows about C's knowledge. A would then reply, "yes, C knows that B has blue eyes." Same thing would happen if we asked about D or E.
If however we asked "what do you think B would answer if I asked him, do you know whether any one of you has blue eyes?", A's answer would be "I don't know". As far as she knows, B is unaware of his own eye color, and while A knows that B knows what A's color is, she doesn't know that exact color.
Then the troll comes and says, "at least one of you has blue eyes." If we were to ask A that last question again, her answer now would be "yes, B knows that there's at least one of us with blue eyes, but I don't know which of us he knows to have blue eyes." Because in her mental model, B can either pin the blue eyes on himself (if he sees no other blue eyed alien) or on A, if he knows her to have blue eyes. A won't know until next morning whether B realized that he's the one with blue eyes. Since B doesn't kill himself, A concludes that he pinned the blue eyes on her- so she realized that B knew she has blue eyes, therefore she knows she has blue eyes and will sadly kill herself next morning.
A similar reasoning, with similar tragic conclusion, is going on inside B's head. If we'd asked him, before the troll made the announcement, "what do you think A would answer if I asked her, do you know whether any one of you has blue eyes?", he'd say "I don't know". After the announcement, it will be yes, but he won't know who she pinned the blue eyes on etc.
The main point is that we've found a question which had an answer before the announcement, and a different answer afterwards. There's your information that the troll conveyed.
The original puzzle formulation usually involved more agents, like 100 blue eyed aliens out of 1000 for example. I won't draw diagrams for puzzles of that magnitude, I'll just show how the same idea generalizes to more aliens by one extra example. Suppose that three out of the five aliens are blue eyed -
and the troll's announcement is the same, "at least one of you has blue eyes". I'll again look inside the mind of A, and to avoid clutter I'll only insist on her mental model of B's mind, in which I'll insist on A's model of B's model of C's mind:
And yes, in A's model of B's model of C's mind, both A and B figure with 'white' eyes- known color, but unknown to some level in the modelling hierarchy. A has white eyes in that model because A knows that everyone else knows her color, but she herself doesn't. And in B's model of C's mind, B's eye color is also white because B doesn't know his own eye color, and A would know that uncertainty and incorporate it into her model of B's mind. I stress again that A's model of B's mind is incomplete. B does know A's color, and A knows that B knows, but she doesn't know that exact color.
So the illuminating question we should now be asking A is, "what do you think B's answer would be if I asked him, what do you think C's answer would be to the question, "do you know if one of you has blue eyes?"
Before the troll speaks, the answer is "I don't know". Look at the picture above to see why. A's model of B's mind is incomplete, and that incompleteness spreads into what she thinks B's model of C's mind is. Our question brings that uncertainty to light.
After the troll speaks, the answer is, of course, yes- because the troll just told everyone. But who does A think that B thinks that C pinned the blue eyes on? Either of the white-eyed figures represents a possible option. Remember that while A knows that C will pin the blue eyes on B, and therefore not kill himself immediately, she doesn't know who B thinks C will pin the blue eyes on.
Since C doesn't kill himself immediately, A now knows that B knows that C knows of a blue eyed alien other than himself. If A had not-blue eyes, then B would know this, and would then suspect that C is seeing B with blue eyes, and the two of them would kill themselves next morning. But that doesn't happen. So now A knows that B knows that C knows there's a blue eyed alien, who isn't either B or C. Which tells A that she has blue eyes.
A similar reasoning is followed by B and C.
One thing to notice is that the deeper one goes into who knows what about whose knowledge, the more uncertainty accumulates. Each of A, B and C knows of two blue eyed aliens. Each of A, B and C knows that each of the other two knows of one blue eyed alien. But, for example, A doesn't know that B knows that C knows of one blue eyed alien.
On the other hand, "at least one of you has blue eyes", when publicly announced, provides information at all layers of recursion. Turns out you can say quite a lot even with words that convey no apparent information, simply by the act of saying this where everyone knows you've said it, and everyone knows that everyone knows that you've said it.
Well, at least if you're talking to perfect deductive intellects. Which is a bit unrealistic.
Just for fun a pretty picture of the situation: our five aliens, A, B, C, D, and E, each with their eye colors.
Now, what's interesting about the puzzle is that one can make two arguments about what happens. Both seem valid, but they can't both be, because their conclusions are contradictory. So one must be wrong, and it is interesting to see why.
I must stress, this is no 'lateral thinking'/'text lawyering' puzzle. It merely concerns itself with what the aliens can deduce from what the troll said. And even if a being that can deduce -every- consequence of something is implausible, that's not the point. These aliens can, so what will they do based on the information provided by the troll?
First answer is- nothing, because the troll gave them no information (ie, didn't tell them anything they didn't already know). "There's at least one blue eyed alien among you": well, each alien can see at least one blue-eyed alien. So all of them already know that what the troll said is true.
Second answer typically proceeds like this:
Terence Tao: We induct on n. When n=1, the single blue-eyed {alien} realizes that the traveler is referring to him or her, and thus commits suicide on the next {morning}. Now suppose inductively that n is larger than 1. Each blue-eyed {alien} will reason as follows: “If I am not blue-eyed, then there will only be n-1 blue-eyed people on this island, and so they will all commit suicide n-1 days after the {troll}’s address”. But when n-1 days pass, none of the blue-eyed people do so (because at that stage they have no evidence that they themselves are blue-eyed). After nobody commits suicide on the(n-1)st day, each of the blue eyed people then realizes that they themselves must have blue eyes, and will then commit suicide on the n-th day.The second answer is in fact correct, but this isn't intuitive as the lively discussion on Terence Tao's blog shows (some other puzzles also have the property of dividing would be solvers). For one thing, people seem suspicious of the inductive argument deployed. And just -what- information could the troll have conveyed, by stating something everyone already knew? Tao asks his readers this precise question, and this post gives an answer, and an alternative solution/argument for the puzzle that agrees with the inductive one.
First thing to note is that often words mean more than what they appear to. Consider a very simple but enlightening scenario presented at the Stanford Encyclopedia of Philosophy: a waiter, as he passes you by, trips on something and spills drinks all over your expensive suit. Immediately the waiter says "I'm sorry, that was my fault" and dashes for a towel to dry you off. It's a pretty safe bet you're already blaming the waiter, and the waiter would know that you already think it's his fault. What you don't know is whether the waiter admits responsibility for clumsiness or is an irresponsible jerk. It's this uncertainty that his apology wants to dispel- the waiter wants you to know that the waiter also knows it was his fault.
Granted, he could have just said "I want you to know that I know that it was my fault", but human communication is often more subtle than meaning just what you say, as we've just seen.
Back to the puzzle. Let's imagine that we could look inside the mind of alien A and see what she knows. Obviously, she knows the eye colors of everyone else and doesn't know her own.
But actually, she knows a bit more. She knows that the other aliens are looking at each other, so she can deduce a few things about what they know, too. So let's update our diagram a bit ...
A few explanations on the drawing's conventions: whenever A knows something, she also knows that she knows that something, and knows that she knows that she knows etc. Since drawing this adds nothing but clutter, the part of the diagram that corresponds to A's self knowledge is marked red and left blank. Likewise, when A knows that B knows something, she also knows that B knows that B knows that something etc. So the part that corresponds to B's self knowledge, as assumed by A, is similarly marked red and left blank. It's trivial to fill these in if one wants to.
Notice also that I use question marks to say that somebody doesn't know their own color. Meanwhile, in the zone in which I drew A's knowledge of what B knows, I put white in B's knowledge of A's eye color. That's because A knows that B knows A's eye color, but what exactly that color is, A doesn't know.
And of course, A knows even more. We can expand that drawing to include knowledge about the knowledge about the knowledge of others. The interested reader may do this, but for this particular puzzle, this is not relevant.
Let's say now that, -before- the troll visited the aliens, we took A to one side, where no other alien is present, and asked her "do you know whether anyone of you has blue eyes"? Let's assume that since no other alien can hear her, the taboo against discussing eye colors is relaxed. Whatever. Her answer is, "yes, for example B has blue eyes."
That was easy. Let's say we asked instead, "what do you think C would answer if I asked him, do you know whether any one of you has blue eyes?". Look at the drawing above and see what A knows about C's knowledge. A would then reply, "yes, C knows that B has blue eyes." Same thing would happen if we asked about D or E.
If however we asked "what do you think B would answer if I asked him, do you know whether any one of you has blue eyes?", A's answer would be "I don't know". As far as she knows, B is unaware of his own eye color, and while A knows that B knows what A's color is, she doesn't know that exact color.
Then the troll comes and says, "at least one of you has blue eyes." If we were to ask A that last question again, her answer now would be "yes, B knows that there's at least one of us with blue eyes, but I don't know which of us he knows to have blue eyes." Because in her mental model, B can either pin the blue eyes on himself (if he sees no other blue eyed alien) or on A, if he knows her to have blue eyes. A won't know until next morning whether B realized that he's the one with blue eyes. Since B doesn't kill himself, A concludes that he pinned the blue eyes on her- so she realized that B knew she has blue eyes, therefore she knows she has blue eyes and will sadly kill herself next morning.
A similar reasoning, with similar tragic conclusion, is going on inside B's head. If we'd asked him, before the troll made the announcement, "what do you think A would answer if I asked her, do you know whether any one of you has blue eyes?", he'd say "I don't know". After the announcement, it will be yes, but he won't know who she pinned the blue eyes on etc.
The main point is that we've found a question which had an answer before the announcement, and a different answer afterwards. There's your information that the troll conveyed.
The original puzzle formulation usually involved more agents, like 100 blue eyed aliens out of 1000 for example. I won't draw diagrams for puzzles of that magnitude, I'll just show how the same idea generalizes to more aliens by one extra example. Suppose that three out of the five aliens are blue eyed -
and the troll's announcement is the same, "at least one of you has blue eyes". I'll again look inside the mind of A, and to avoid clutter I'll only insist on her mental model of B's mind, in which I'll insist on A's model of B's model of C's mind:
And yes, in A's model of B's model of C's mind, both A and B figure with 'white' eyes- known color, but unknown to some level in the modelling hierarchy. A has white eyes in that model because A knows that everyone else knows her color, but she herself doesn't. And in B's model of C's mind, B's eye color is also white because B doesn't know his own eye color, and A would know that uncertainty and incorporate it into her model of B's mind. I stress again that A's model of B's mind is incomplete. B does know A's color, and A knows that B knows, but she doesn't know that exact color.
So the illuminating question we should now be asking A is, "what do you think B's answer would be if I asked him, what do you think C's answer would be to the question, "do you know if one of you has blue eyes?"
Before the troll speaks, the answer is "I don't know". Look at the picture above to see why. A's model of B's mind is incomplete, and that incompleteness spreads into what she thinks B's model of C's mind is. Our question brings that uncertainty to light.
After the troll speaks, the answer is, of course, yes- because the troll just told everyone. But who does A think that B thinks that C pinned the blue eyes on? Either of the white-eyed figures represents a possible option. Remember that while A knows that C will pin the blue eyes on B, and therefore not kill himself immediately, she doesn't know who B thinks C will pin the blue eyes on.
Since C doesn't kill himself immediately, A now knows that B knows that C knows of a blue eyed alien other than himself. If A had not-blue eyes, then B would know this, and would then suspect that C is seeing B with blue eyes, and the two of them would kill themselves next morning. But that doesn't happen. So now A knows that B knows that C knows there's a blue eyed alien, who isn't either B or C. Which tells A that she has blue eyes.
A similar reasoning is followed by B and C.
One thing to notice is that the deeper one goes into who knows what about whose knowledge, the more uncertainty accumulates. Each of A, B and C knows of two blue eyed aliens. Each of A, B and C knows that each of the other two knows of one blue eyed alien. But, for example, A doesn't know that B knows that C knows of one blue eyed alien.
On the other hand, "at least one of you has blue eyes", when publicly announced, provides information at all layers of recursion. Turns out you can say quite a lot even with words that convey no apparent information, simply by the act of saying this where everyone knows you've said it, and everyone knows that everyone knows that you've said it.
Well, at least if you're talking to perfect deductive intellects. Which is a bit unrealistic.




Comments
Post a Comment