The BLAND Corporation

It's no secret by now to anyone not living under a rock that Prometheus the movie has been in cinemas, where it left a rather ... meh impression. Or rather, hostility. The film has many vocal detractors; I understand where they're coming from. I still love the film.

Oh look, 15th post! Significant because any post beyond this arbitrary threshold which I've arbitrarily set will cause an "older posts" link to appear. Time to experiment a bit with these newfangled inventions called "tags". I wonder what they do. Update: what the hell? I make one post with the tag 'Prometheus' and it quickly gets 20 hits from google.co.uk. That's fairly unimpressive on its own (though compared with the other posts' viewcounts, astronomical), but what's odd is that the google search in question was for 'Prometheus stream'. If you came here looking for that I must apologize.

Back in the 1960s, Joseph Weizenbaum made some of the first chatterbots. Some excerpts from conversations between those bots and human beings can be found here . What was rather peculiar, despite knowing that the bots were bots, many users felt an emotional connection of some kind developing. Even if there was nothing on the bot's part to support such a thing. Even if the human participant knew that. That turn of events is particularly interesting to me and my 'mind-likeness' program , as it shows a few things ... 1. Human beings are very keen on/easily tricked into applying mind-likeness/intentional stance. However, the fact that spurious correlations may appear between unrelated phenomena does not make correlation a useless statistical tool, and similarly mind-likeness/intentional stance is often useful to deploy. All the more reason to understand how to deploy it correctly. 2. The nature of the trickery appears misunderstood in the accounts of the experiment. It do

A recent post dealt with a puzzle involving perfect deductive intellects, beings who could, instantly, deduce every possible implication of their current state of knowledge. Obviously, it's not something that can be achieved with physical computers nor brains. Indeed, there's at least one whole art form concerning itself with the control of how people allocate their cognitive resources. So it's not too insightful to suggest that any model of a human mind -or any mind- needs to account for that mind's limitations. The problem is not just one of limited resources. In particular, in some regards the human mind is patently weird, as a few other puzzles show.

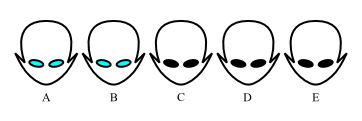
Here's a nifty gem of epistemic logic, a little puzzle that crops around in many forms. It appears at Terence Tao's blog , there's also an xkcd page about it , and there are several variations on it. Consider this one, simpler but complex enough to capture the subtlety: suppose there's a group of five aliens who are highly logical beings (whatever one can deduce, will be immediately deduced by that alien) but also rather quirky. None of them know the color of their own eyes, they don't speak with each other about eye colors, and they live where no reflective surfaces or such will ever tell them that information. So each alien knows only the colors of the others' eyes and not their own. If it matters, possible eye colors that the aliens know about are blue, green, red, black. As it happens, two out of the aliens in the group have blue eyes, and the remaining three have black eyes. A further quirk of these aliens: if ever one of them discovers the color of his/her

Toyed a bit with the Graph parts of BOOST C++. Very useful tool, I'll need to learn more of it. So far, I've revisited an older post from this blog . A brief recap: in some grid of 'workshops'/'research centers' that are making their way up a tech tree by discovery and/or knowledge transfer from their neighbors, workshops that are closer to the center of the grid/farther away from obstacles to knowledge transfer are more likely to reach the top of the tree first. For some general graph, not just a grid, what measure of centrality would capture this behaviour?

A few days ago, Felix Baumgartner flew in a Helium-filled balloon to an altitude of 39 kilometers and then jumped out. The data is being pored over by the FAI to get the exact figures, but he did indeed perform the highest to date manned ascent in a balloon and highest parachute jumped, achieved supersonic velocity while free-falling, and the longest recorded free fall distance, but not longest free fall time- that record still belongs to Joseph Kittinger, the first man to do a sky dive from the stratosphere in 1960. Kittinger also served as the ground-based adviser to Baumgartner today, a nice passing the torch moment. Baumgartner's jump was a nifty Red Bull project, a daredevil stunt and good tv (hey I liked it loads). Back in Kittinger's day, there was another concern- would an astronaut be able to bail out of a malfunctioning craft and get to ground safely?

I recently received a link to an article by David Deutsch about why Artificial General Intelligence (allegedly) is going nowhere even though by all indication it should be possible. One thing about that and the discussion it generated is fairly uncontroversial: the problem of what intelligence means is so ill specified so as to make any answer pointless. I don't think it's the case that AGI has been standing still, but for every new, and genuinely cool development, the usual response is that it's just some small task part of a larger unknown whole. If we have a clearly defined problem (like, say, make suggestions for other items of potential interest on amazon.com) then we can make progress. If the problem is ill-defined, one can always shift the goal-posts. Which results in discussions about consciousness and intelligence and the meaning of it all that are actually rather sterile, merely occasions for the posters to sound smart. At least in their own eyes. I can certain

There's a tendency for creative types living in the West to pat themselves on the back, "at least we don't have to work under the constraints imposed by Soviet propaganda". True, but not quite a complete picture. Censorship has many forms, many disguised by the mechanisms that power the publishing and distribution industry, and it can be found everywhere, including in countries that value freedom of speech. Conversely, how censorship manifested itself in the Soviet world and its satellites varied from place to place and time to time. It wasn't necessarily the case that an unpleasant author would find themselves with a new unwanted hole in their head, or splitting rocks in some frozen wasteland.